- Published on
🔍 Chiến lược tìm kiếm không thông tin
- Authors

- Name
- Nguyễn Văn Lộc
- @vanloc1808
🔍 Thuật toán tìm kiếm
Có nhiều cách để giải quyết vấn đề bằng máy tính. Điều kiện chính để giải quyết một vấn đề là chúng ta phải biểu diễn thành công vấn đề đó. Bài viết này thảo luận về các chiến lược tìm kiếm không thông tin, có nghĩa là chúng ta không có thông tin nào khác ngoài các điều kiện của vấn đề.
🗺️ Biểu diễn các vấn đề tìm kiếm
Một vấn đề thường chứa các yêu cầu và giải pháp. Tìm kiếm được sử dụng để tìm ra giải pháp trong không gian tìm kiếm.
Một vấn đề tìm kiếm thường chứa năm thành phần:
- 🌐 Không gian trạng thái: tất cả các trạng thái có thể của vấn đề.
- 🚀 Trạng thái ban đầu: trạng thái mà từ đó việc tìm kiếm bắt đầu, ví dụ, người đó sẽ bắt đầu từ Thành phố Hồ Chí Minh.
- 🔄 Mô hình chuyển đổi: một hàm nhận một trạng thái và trả về một tập hợp các trạng thái có thể đạt được từ trạng thái đã cho.
- 🎯 Trạng thái mục tiêu: trạng thái mà chúng ta muốn đạt được, ví dụ, người đó muốn đi đến Hà Nội.
- 💰 Chi phí đường đi: một hàm gán chi phí số cho mỗi đường đi.
🌐 Không gian trạng thái
Để giải quyết một vấn đề tìm kiếm, chúng ta cần định nghĩa không gian trạng thái phù hợp. Dựa trên trạng thái ban đầu và mô hình chuyển đổi, chúng ta có thể xác định tất cả các trạng thái có thể đạt được, vì vậy chúng ta có thể hiểu rằng không gian trạng thái là tất cả các trạng thái có thể đạt được từ trạng thái ban đầu.
Không gian trạng thái thường được biểu diễn bằng một đồ thị, vì vậy chúng ta gọi là đồ thị không gian trạng thái. Trong đồ thị này:
- Mỗi nút đại diện cho một trạng thái.
- Mỗi cạnh đại diện cho một chuyển đổi từ trạng thái này sang trạng thái khác. Ví dụ, xem xét Vấn đề người bán hàng rong. Biểu diễn đồ thị của nó như sau.
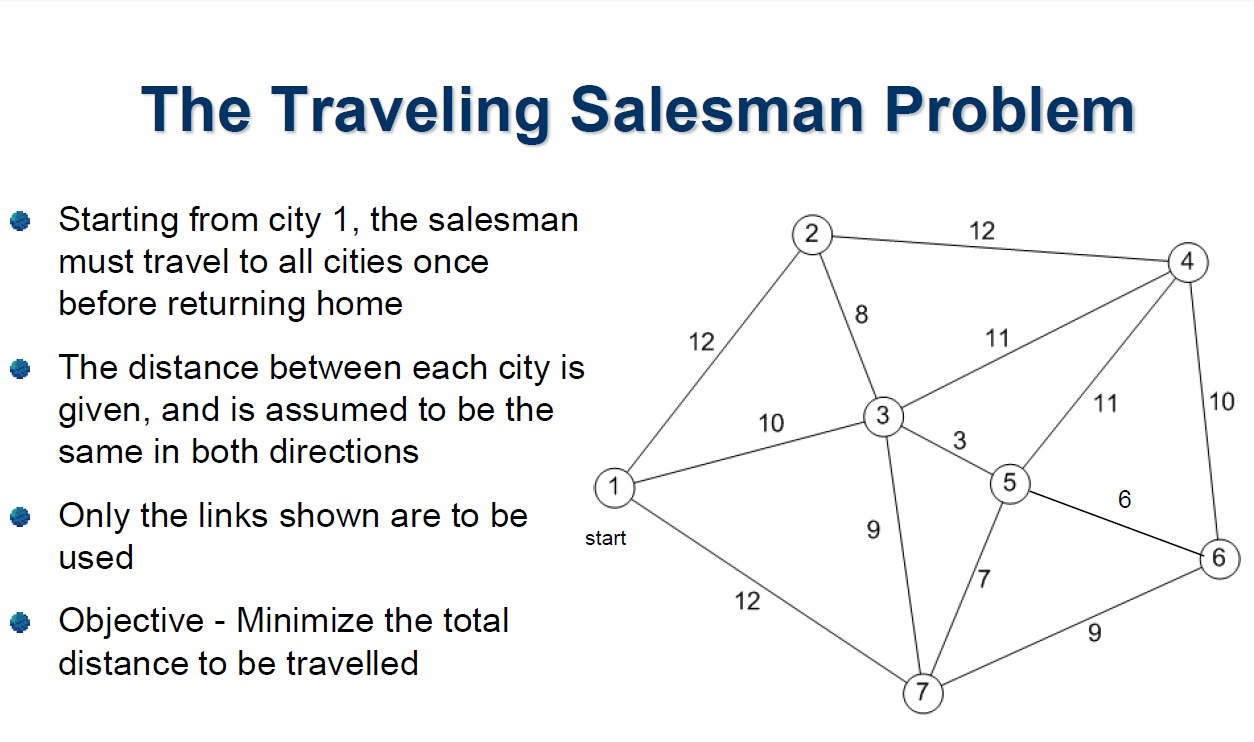
📍 Trạng thái
Trạng thái trong vấn đề tìm kiếm là biểu diễn của vấn đề tại một thời điểm cụ thể. Trạng thái được biểu diễn bằng một nút trong đồ thị không gian trạng thái.
Ví dụ, trong Vấn đề người bán hàng rong, một trạng thái là một thành phố mà người bán hàng hiện đang ở.
🔄 Mô hình chuyển đổi
Mô hình chuyển đổi là một hàm nhận một trạng thái và trả về một tập hợp các trạng thái có thể đạt được từ trạng thái đã cho. Mô hình chuyển đổi được biểu diễn bằng các cạnh trong đồ thị không gian trạng thái.
💰 Chi phí đường đi
Chi phí đường đi là một hàm gán chi phí số cho mỗi đường đi. Chi phí đường đi được biểu diễn bằng chi phí (trọng số) của các cạnh trong đồ thị không gian trạng thái.
🎮 Ví dụ về vấn đề tìm kiếm
🚛 Vấn đề người bán hàng rong (TSP)
Vấn đề người bán hàng rong là một vấn đề tối ưu hóa cổ điển. Vấn đề là tìm ra tuyến đường ngắn nhất có thể mà thăm mỗi thành phố chính xác một lần và trở lại thành phố ban đầu.
♛ Vấn đề 8 quân hậu
Vấn đề 8 quân hậu là một vấn đề cổ điển trong đó mục tiêu là đặt 8 quân hậu trên bàn cờ 8x8 sao cho không có hai quân hậu nào đe dọa nhau.
🌊 Tìm kiếm theo chiều rộng (BFS)
🌊 Chiến lược BFS
Mở rộng nút theo từng cấp độ, như gợn sóng lan rộng trong nước
Tìm kiếm theo chiều rộng (BFS) là việc mở rộng cây tìm kiếm theo chiều rộng. Nút gốc sẽ được xem xét ban đầu, sau đó, tất cả các nút con của nút gốc sẽ được mở rộng. Sau đó, tất cả các nút con của các nút con của nút gốc sẽ được mở rộng, và cứ thế tiếp tục.
💡 Insight chính: BFS đảm bảo tìm đường đi ngắn nhất (về số bước) trước tiên!
Triển khai Python của thuật toán BFS như sau:
def bfs(graph, start, goal):
explored = []
queue = [[start]]
if start == goal:
return "Start is the goal"
while queue:
path = queue.pop(0)
node = path[-1]
if node not in explored:
neighbors = graph[node]
for neighbor in neighbors:
new_path = list(path)
new_path.append(neighbor)
queue.append(new_path)
if neighbor == goal:
return new_path
explored.append(node)
return "No path found"
💰 Tìm kiếm chi phí đồng nhất (UCS)
💰 Chiến lược UCS
Luôn mở rộng nút có chi phí thấp nhất trước
Một trong những nhược điểm chính của BFS là nó không xem xét chi phí của đường đi. Tìm kiếm chi phí đồng nhất (UCS) là một phần mở rộng của BFS có xem xét chi phí của đường đi.
⚡ Insight chính: UCS tìm đường đi tối ưu với chi phí tối thiểu!
Triển khai Python của thuật toán UCS như sau:
def ucs(graph, start, goal):
explored = []
queue = [[start]]
if start == goal:
return "Start is the goal"
while queue:
path = queue.pop(0)
node = path[-1]
if node not in explored:
neighbors = graph[node]
for neighbor in neighbors:
new_path = list(path)
new_path.append(neighbor)
queue.append(new_path)
if neighbor == goal:
return new_path
explored.append(node)
queue = sorted(queue, key=lambda x: sum(x))
return "No path found"
🏔️ Tìm kiếm theo chiều sâu (DFS)
🏔️ Chiến lược DFS
Đi sâu trước, như khám phá hệ thống hang động
Không giống như BFS, Tìm kiếm theo chiều sâu (DFS) mở rộng cây tìm kiếm theo chiều sâu.
🎯 Insight chính: DFS sử dụng ít bộ nhớ hơn nhưng có thể không tìm được đường đi ngắn nhất!
Triển khai Python của thuật toán DFS như sau:
def dfs(graph, start, goal):
explored = []
stack = [[start]]
if start == goal:
return "Start is the goal"
while stack:
path = stack.pop()
node = path[-1]
if node not in explored:
neighbors = graph[node]
for neighbor in neighbors:
new_path = list(path)
new_path.append(neighbor)
stack.append(new_path)
if neighbor == goal:
return new_path
explored.append(node)
return "No path found"
🔄 Tìm kiếm làm sâu lặp (IDS)
🔄 Chiến lược IDS
Tốt nhất của cả hai thế giới: tính đầy đủ của BFS + hiệu quả bộ nhớ của DFS
Tìm kiếm làm sâu lặp (IDS) là sự kết hợp của BFS và DFS. Nó có thể tối ưu hóa độ phức tạp thời gian của BFS và độ phức tạp không gian của DFS.
🚀 Insight chính: IDS cho bạn đảm bảo của BFS với hiệu quả bộ nhớ của DFS!
Triển khai Python của thuật toán IDS như sau:
def ids(graph, start, goal):
for depth in range(1, len(graph)):
result = dls(graph, start, goal, depth)
if result:
return result
return "No path found"
📊 So sánh thuật toán
| Thuật toán | Độ phức tạp thời gian | Độ phức tạp không gian | Tối ưu? | Đầy đủ? |
|---|---|---|---|---|
| 🌊 BFS | O(b^d) | O(b^d) | ✅ (không có trọng số) | ✅ |
| 💰 UCS | O(b^(C*/ε)) | O(b^(C*/ε)) | ✅ | ✅ |
| 🏔️ DFS | O(b^m) | O(bm) | ❌ | ❌ (không gian vô hạn) |
| 🔄 IDS | O(b^d) | O(bd) | ✅ (không có trọng số) | ✅ |
Trong đó: b = hệ số phân nhánh, d = độ sâu của giải pháp, m = độ sâu tối đa, C* = chi phí tối ưu, ε = chi phí bước tối thiểu
📚 Tài liệu tham khảo
https://www.geeksforgeeks.org/state-space-search-in-ai/ https://stanford-cs221.github.io/autumn2024/ Artificial Intelligence: A Modern Approach, Stuart Russell and Peter Norvig
📧 Liên hệ
Nếu bạn có bất kỳ câu hỏi hoặc phản hồi nào, hãy liên hệ với tôi.
🎯 Hãy nhớ
Chọn thuật toán tìm kiếm của bạn dựa trên các ràng buộc vấn đề: yêu cầu về bộ nhớ, tính tối ưu, và tính đầy đủ!
🙏 Lời cảm ơn
Cảm ơn ChatGPT đã cải thiện bài viết này với các gợi ý, định dạng và biểu tượng cảm xúc.